How To Square An Area Is An Essential ManMade Skill
As Huey Lewis and the News once sang, “It’s hip to be square” and that relates more than anything if you’re creating a project from scratch. If your walls aren’t square, your home, shed, garage, or any other structure is compromised. Compromised meaning it might just fall down. We’ve all seen those quaint forgotten sheds along an old country road leaning away from the prevailing wind. Quaint they are, but how many people want to live in one.

“What’s so cool about being square?”

Hypotenuse, it’s a strange name for a very useful tool that comes down to us from the ancient Greeks. The Greek word is similar “hypoteinousa” it is defined as stretching under, which is a very appropriate term for what we’re about to discuss.
In our world of vertical, horizontal, and diagonal, the squaring of things has become imperative. When you hang that picture on the wall if the sides don’t align with the ceiling and the surrounding walls, windows, and doors it can drive some people to the brink of insanity.
There are a couple of ways to create a perfectly proportional rectangle (remember 8th-grade math, all squares are rectangles, but not all rectangles are squares) using diagonals.
Pythagoras in the 21st Century
The Pythagorean Theorem is perhaps the best-remembered lesson from geometry class. If you take a right triangle, meaning one angle has to equal 90 degrees, you can determine a third side from two known sides.
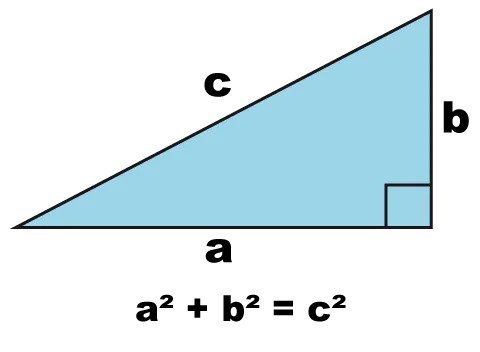
The easiest example is a 3-4-5 right triangle. Let’s say you’re building a deck that is 6×8 feet and you want it square. Start at one point parallel to an existing straight line on your house. Mark two spots, one at the starting point, and another four feet away. You’ll need a partner for the next step. One of you set a measuring tape at three feet, the other at five feet. Connect the ends of the tape to the two points four feet apart, swing the tape until the three and foot marks intersect. You’ve made a 3-4-5 right triangle, more importantly, you’ve created a right angle and have two sides of your deck squared. Switch to the other side and repeat the process. When you’re done you’ll have a 3×8 rectangle. You can simply extend the three-foot side with a string and mark the six-foot corner.

The magic of this method is that the Pythagorean Theorem works perfectly with multiples of 3-4-5 as well. Larger sections of lawn, garden, or the footing of a new building can use 6-8-10, 12-16-20, or any equal multiple of 3-4-5. The process is the same, just the measurements are longer, but the results will be a perfectly squared area.
All Diagonals are Created Equal (or should be when you’re finished)
The other method of squaring with a diagonal is most often used in the shop. When building tables, picture frames, or cabinets it is important to get things completely square, which means parallel lines at right angles to each other.
Set four pieces of wood together that you’re planning to overlap into a rectangle. Two sides could be 24 inches and the other two 18 inches. The lengths don’t matter, what does matter is the diagonal between the two sets of boards.
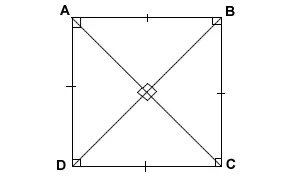
Let’s the four corners A-B-C-D, line AB is opposite line CD, AD and BC are the sides. Measure from the corner of A to the corner of C, remember the measurement. Measure corner B to corner D, if the measurements are the same, your frame is square. If A to C is longer than B to D, you need to slide A and B towards side AD. Repeat the process until the two diagonal measurements are equal and you’ve created four perfect right angles.
Using our 24 and 18-inch examples, the diagonal will be exactly 30 inches. Get that both ways and you’re done!
The End Result of Correct Angles

Right angles in concert can create beautiful wood projects like the one above. You’ll notice that all six surfaces on this planter box are formed by rectangles.